二叉树的遍历
本文中,我将要介绍一下关于二叉树遍历的先关知识,包括bfs和dfs,以及递归等方法。这些知识和题目在初学时可能有些难度,但通过循序渐进的学习,每天的积累也能done it.我在写这篇文章的时候也发现之前忽略的细节,也收获不少。
遍历二叉树:是按照某条搜索路径巡访树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。常见的遍历方法有先序遍历,中序遍历和后序遍历。这三种遍历方法通过树的结构用递归可以简单实现,非递归方法可以用栈和队列。下面从层序遍历开始讲起。
Leetcode102二叉树的层序遍历
有一个二叉树的根结点root,返回其结点值的层序遍历。即逐层地,从左到右访问所有节点。
eg.输入:root=[3,9,20,null,null,15,7]。输出:[[3],[9,20],[15,7]]
题目分析
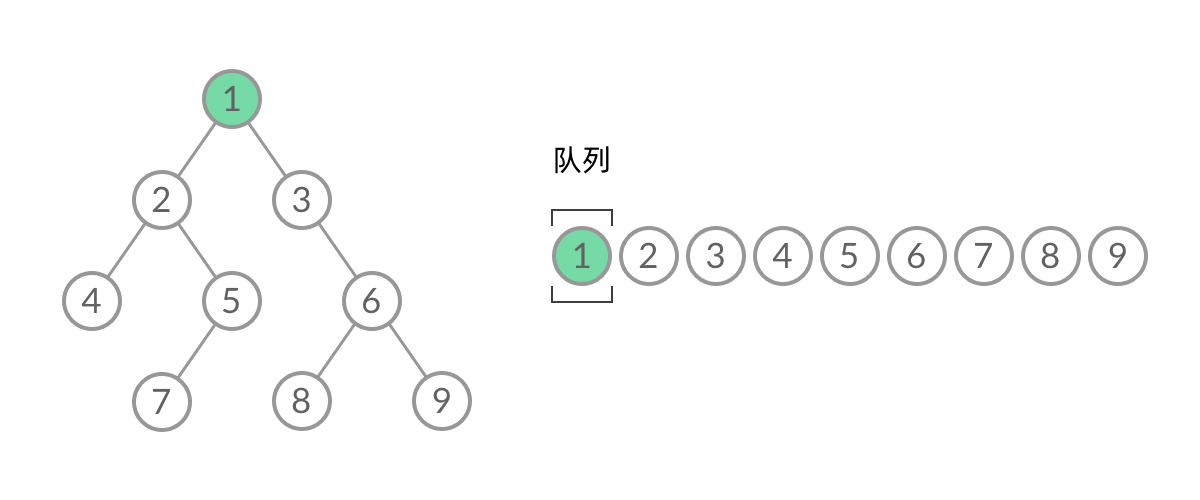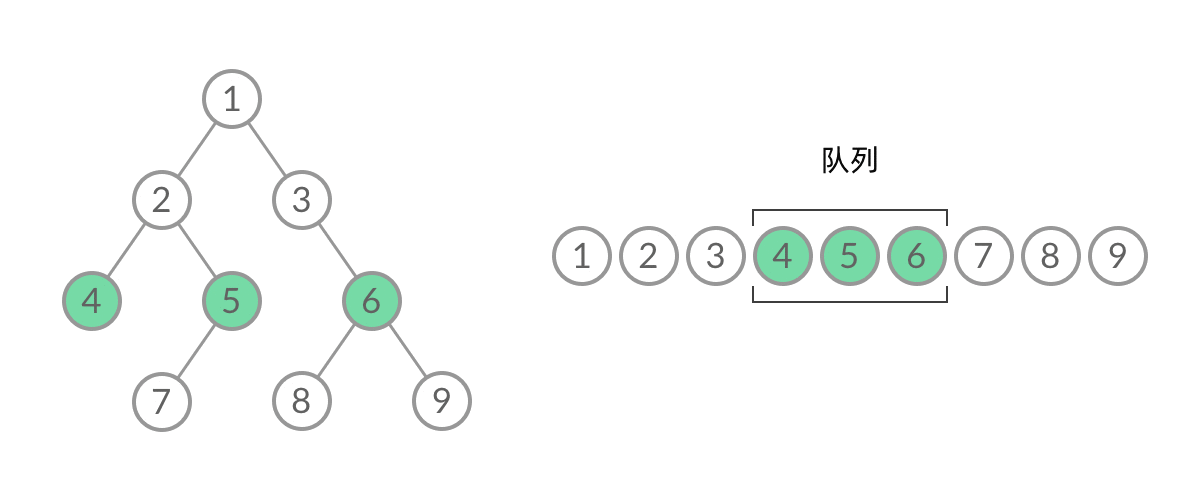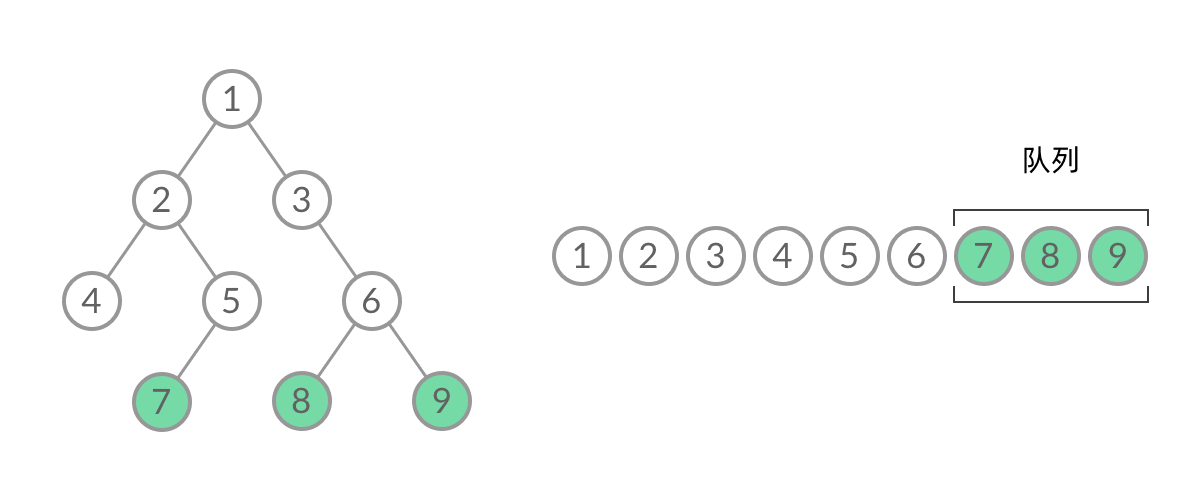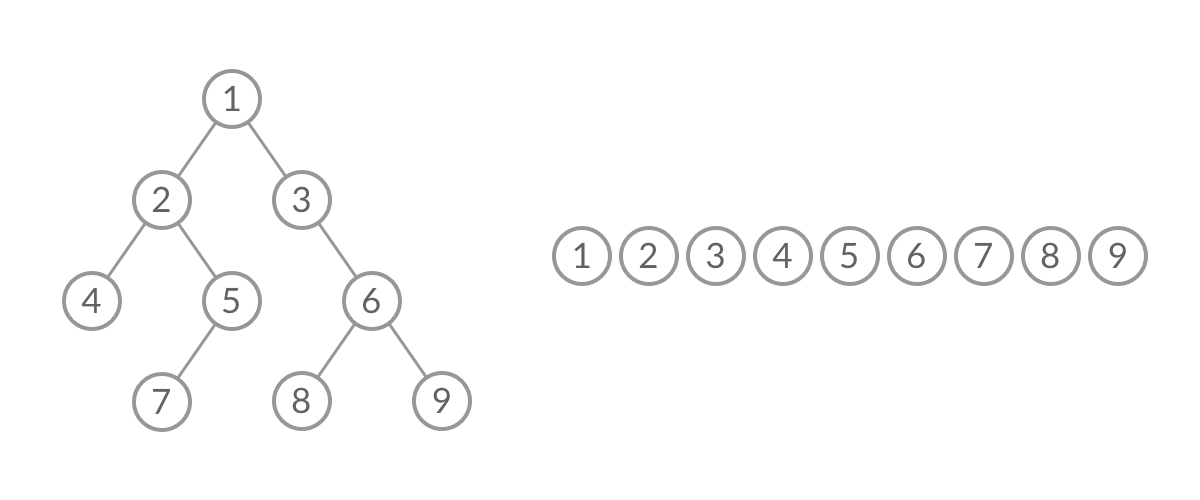
层序遍历是一种典型的广度优先搜索方法,可以通过队列先进先出的性质来进行层序遍历(当一个节点的左右节点入栈后,将其本身弹出栈),如下图所示:
vector<vector<int>>levelOrder(TreeNode *root)
{
vector<vector<int>>ans;
queue<TreeNode*>q;
if(root!=nullptr)
{
q.push(root);
}
while(!q.empty())
{
vector<int>ret;
int n=q.size();
for(int i=0;i<n;i++)
{
TreeNode*now=q.front();
int val=now->val;
q.pop();
ret.push_back(val);
if(now->left!=nullptr) q.push(now->left);
if(now->right!=nullptr) q.push(now->right);
}
ans.push_back(ret);
}
return ans;
}在答案中要求的是一层在一个向量中,所以在此加了一个for循环,循环的次数是根据队列中元素的数量确定的,当把本来位于队列中的元素弹出去后也就意味着下一层的都入队了。
与之类似的leetcode103和leetcode107可以通过相同的方法解决。
Leetcode104 二叉树的最大深度
二叉树的最大深度是指从根节点到最远叶子结点的最长路径上的结点数。
题目分析
一般来说二叉树相关的题目绝大部分都是可以用递归来解决的,递归可以理解成是树深度优先搜索。递归就是将一个问题分解成更小的子问题,把握两个核心要点:
- 核心在于拆分问题,每次调用都是在解决更小的子问题。在二叉树中一般是将父节点相关的问题转化成左右子节点的问题。
- 递归必须有终止条件,把终止条件先确定好。在二叉树中一般为某个节点为空,或该节点的左右子结点均为空。
当然,我比较提倡一题多解,这道题也可以用广度优先搜索解决,和上个题的代码基本一致,只需要在每次for循环后加1即可。
对这道题目而言,递归的终止条件是该节点时空的;拆分成子问题就是求左子树和右子树的深度,哪个深就取哪个,然后再加上1(父节点也占一个高度)。
代码部分
- 深度优先(递归)
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}求链表的长度和这个类似
- 广度优先(队列)
int maxDepth(TreeNode*root)
{
queue<TreeNode*>q;
if(root!=nullptr)
{
q.push(root);
}
int ans=0;
while(!q.empty())
{
int n=q.size();
for(int i=0;i<n;i++)
{
TreeNode*now=q.front();
q.pop();
if(now->left) q.push(now->left);
if(now->right) q.push(now->right);
}
ans+=1;
}
return ans;
}二叉树的最小深度
最小深度是从根节点到最近叶子结点的最短路径上结点的数量。
题目分析
用递归的话,终止条件就是该节点为空。怎么拆分子问题呢?求左子树和右子树上的最小深度,然后再取较小的一个。那么看一下以下代码是否正确:
int minDepth(TreeNode*root)
{
if(root==nullptr) return 0;
return min(minDepth(root->left),minDepth(root->right),INT_MAX)+1;
}这个是我一开始的想法,这个是不正确的,我们想一种情况,就是如果一棵树只有右子节点,那么这个代码的结果就是1,因为minDepth(root->left)=0。那么这个不是我们想要得到的结果。一个非空的节点存在三种状态:1.左右子节点均存在。2.左子节点存在右子节点不存在。3.右子节点存在左子节点不存在。如果是情况1的话,上面的return后面的代码是没有问题的。如果是另外两种情况呢,一个节点的深度是0,另一个的是m(一个大于0的数),我们想取m,所以直接max(minDepth(root->left),minDepth(root->right))+1即可,完整代码看下方:
int minDepth(TreeNode*root)
{
if(root==nullptr) return 0;
if(root->left !=nullptr &&root->right!=nullptr) return min({minDepth(root->left),minDepth(root->right),INT_MAX})+1;
else return max(minDepth(root->left),minDepth(root->right))+1;
}广度优先的话还是用队列
int minDepthbfs(TreeNode*root)
{
queue<TreeNode*>q;
if(root!=nullptr) q.push(root);
int ans=0;
while(!q.empty())
{
int n=q.size();
for(int i=0;i<n;i++)
{
TreeNode*now=q.front();
q.pop();
if(now->left==nullptr && now->right==nullptr)
{
return ans+1;
}
if(now->left!=nullptr) q.push(now->left);
if(now->right!=nullptr) q.push(now->right);
}
ans+=1;
}
return ans;
}leetcode101对称二叉树
给你一个二叉树的根结点root,检查它是否轴对称。
eg.输入:root=[1,2,2,3,4,4,3],输出:true
输入:root=[1,2,2,null,3,null,3],输出:false
题目分析
这棵树是否对称,在于根结点的左子树和右子树是否为镜像关系,所先把研究对象从整棵树变成左右子树。
- 深度优先搜索(递归)
- 终止条件,若左子树和右子树对应位置均为空,则符合;若左子树和右子树对应位置一个是空,一个不是空,则不符合,对应位置的值是不相等也是不符合。
- 拆分成子问题,若当前比较的是结点p和q,那么子问题就是比较p->left和p->right 以及 p->right 和p->left。
bool check(TreeNode*p,TreeNode*q)
{
if(p==nullptr && q==nullptr) return true;
if(p!=nullptr && q!=nullptr) return true;
return (p->val==q->val) &&check(p->left,q->right) && check(p->right,q->left);
}
bool isSymmetric(TreeNode*root)
{
return check(root->left,root->right);
}- 广度优先(队列)
bool isSymmetric(TreeNode *root)
{
if(root==nullptr ||(root->left==nullptr && root->right==nullptr))
{
return true;
}
queue<TreeNode*>q;
q.push(root->left);
q.push(root->right);
while(q.size()>0)
{
TreeNode*left=q.front();
q.pop();
TreeNode*right=q.front();
q.pop();
if(left==nullptr && right==nullptr)
{
continue;
}
if(left==nullptr || right==nullptr)
{
return false;
}
if(left->val!=right->val)
{
return false;
}
q.push(left->left);
q.push(right->right);
q.push(left->right);
q.push(right->left);
}
return true;
}这两个方法的相似之处就是比较left->left与right->right 以及left->right和right->left是否相等,这也是这道题的本质所在。
leetcode112路径总和1
有一个二叉树的根节点root和一个表示目标和的整数targetSum。判断该树中是否存在根节点到叶子结点的路径,这条路径上所有节点值相加等于目标和targetSum。如果存在,返回trur;否则,返回false。
题目分析
所有节点的值相加等于目标和,这个就要求我们在遍历节点的时候,需要记录从从节点到该节点的路径和,到叶子结点的时候再判断路径和是否等于目标值。
- 深度优先搜索(递归)
- 拆分子问题:root的左右结点到叶子结点的路径和是否等于target-root->val。
- 终止条件:叶子结点的值是否等于target减去它所有祖先节点的值(不包括它自己)。
bool hasPathSum(TreeNode*root,int sum)
{
if(root==nullptr) return false;
if(root->left==nullptr &&root->right==nullptr)
{
return root->val==sum;
}
return (hasPathSum(root->right,sum-root->val) ||hasPathSum(root->left,sum-root->val));
}
- 广度优先搜索(队列)
之前有队列来对二叉树进行层序遍历的时候,是用了一个队列将整个二叉树进行了层序遍历,没有计算路径和。我们可以再建立一个队列,来存储到从根节点到相应结点的路径和,并判断 如果是叶子结点的话是否等于路径和。
bool hasPathSumque(TreeNode*root,int target)
{
queue<TreeNode*>q_node;
queue<int>q_value;
if(root!=nullptr)
{
q_node.push(root);
q_value.push(root->val);
}
while(!q_node.empty())
{
int n=q_node.size();
for(int i=0;i<n;i++)
{
TreeNode*now_node=q_node.front();
int now_value=q_value.front();
q_node.pop();q_value.pop();
if(now_node->left==nullptr && now_node->right==nullptr && now_value==target)
{
return true;
}
if(now_node->left!=nullptr)
{
q_node.push(now_node->left);
q_value.push(now_node->left->val+now_value);
}
if(now_node->right!=nullptr)
{
q_node.push(now_node->right);
q_value.push(now_node->right->val+now_value);
}
}
}
return false;
}leetcode113路径总和2
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
eg.输入:root =[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22。输出:[[5,4,11,2],[5,8,4,5]]
题目分析
此题的困难点在于需要找出完整的路径,如果用深度优先搜索的方法,需要用到回溯。从根节点开始,我们创建一个向量开始存储节点的值,当到第一个根结点的时候(左下侧的根节点),先看是否是目标路径,然后将最后一个元素弹出向上回溯,再到其他根结点。如果用广度优先搜索,我们可以在将左右子结点入队的时候用哈希表将其父节点存储起来,当找到对应的目标叶子结点的时候,再一步一步的找其父节点。
- 深度优先搜索(递归)
- 终止条件:该节点是叶子结点,并且路径和满足目标值。
- 拆分子问题:该节点的左右子节点和新的target。
- 还要注意的是需要从左下角的叶子节点回溯到右下角的叶子节点。
class Deepfirst
{
public:
vector<vector<int>>ret;
vector<int>path;
void dfs(TreeNode*root,int target)
{
if(root==nullptr)
{
return ;
}
path.push_back(root->val);
target-=root->val;
if(root->left==nullptr && root->right==nullptr &&target==0)
{
ret.push_back(path);
}
dfs(root->left,target);
dfs(root->right,target);
path.pop_back();
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum)
{
dfs(root,targetSum);
return ret;
}
};比较重要的一点是需要从叶子结点回溯到叶子结点。
- 广度优先搜索(队列)
用广度优先搜索的时候,如果我们想从叶子结点回溯到头结点,那就需要在结点入队的时候用哈希表将结点对应的父节点存储起来,方便回溯。
class Solution
{
public:
vector<vector<int>> ret;
unordered_map<TreeNode*,TreeNode*>parent;
void getpath(TreeNode*node)
{
vector<int>temp;
while(node)
{
temp.push_back(node->val);
node=parent[node];
}
reverse(temp.begin(),temp.end());
ret.push_back(temp);
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum)
{
queue<TreeNode*>q_node;
queue<int> q_value;
if(root!=nullptr)
{
q_node.push(root);
q_value.push(root->val);
}
while(!q_node.empty())
{
int n=q_node.size();
for(int i=0;i<n;i++)
{
TreeNode*now_node=q_node.front();
int now_value=q_value.front();
q_node.pop();q_value.pop();
if(now_node->left==nullptr && now_node->right==nullptr)
{
if(now_value==targetSum)
{
getpath(now_node);
}
}
if(now_node->left!=nullptr)
{
parent[now_node->left]=now_node;
q_node.push(now_node->left);
q_value.push(now_node->left->val+now_value);
}
if(now_node->right!=nullptr)
{
parent[now_node->right]=now_node;
q_node.push(now_node->right);
q_value.push(now_node->right->val+now_value);
}
}
}
return ret;
}
};这个代码可能有一点长,我来捋一下,一开始是层序遍历,用到了一个队列来存储节点,然后是路径总和1,又增加了一个队列用来存储从头结点到该节点的路径和,再就是这道题,在将结点入队的同时又记录该节点的父结点,并加上了回溯的操作。