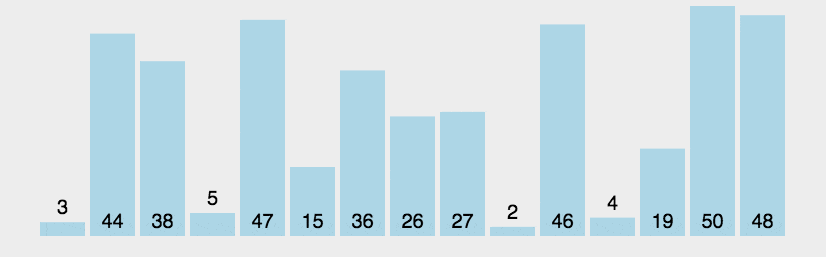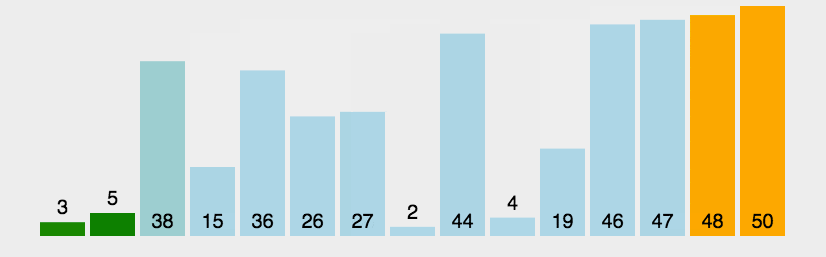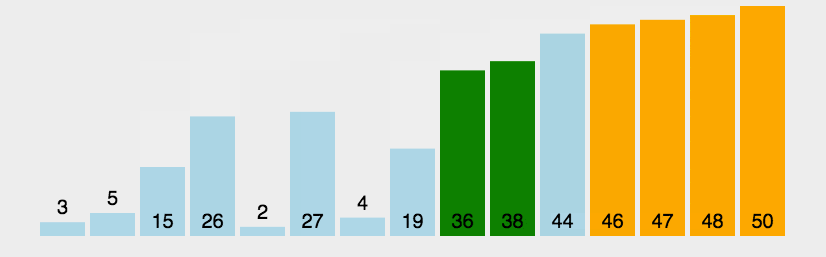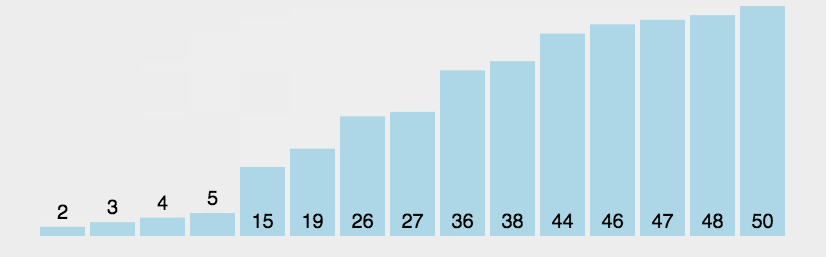十大排序算法
在本文中,我将介绍10种经典的排序方法,一个很简单的排序,却有很多方法可以解决,每种方法也各有优缺点,每种方法也体现了一种思想,我认为算法中最重要的就是学会一些思想,这样才能做到以不变应万变。本文中的代码均是使用的C/C++(文章中的动图参考 https://github.com/hustcc/JS-Sorting-Algorithm 。若是侵权,我立刻删除)
冒泡排序
算法思想
- 从列表第一个元素开始,比较相邻两个元素值的大小,让小的到前面。
- 当遍历完一轮后,最大的元素就已经到最后一个了,所以共需遍历n-1次。
动图展示
代码部分
#include<iostream>
using namespace std;
void bubblesort(int data [],int n)
{
int temp;
for(int j=0;j<n-1;j++)
{
for(int i=0;i<n-1;i++)
{
if(data[i]>data[i+1])
{
temp=data[i];
data[i]=data[i+1];
data[i+1]=temp;
}
}
}
}
int main()
{
int a;
cin>>a;
int*b=new int[a];
for(int i=0;i<a;i++)
{
cin>>b[i];
}
bubblesort(b,a);
for(int j=0;j<a;j++)
{
cout<<b[j]<<" ";
}
delete []b;
}这个代码理解起来很容易,n个数需要进行n-1轮遍历,每轮遍历需要进行n-1次,然后就是比较大小,让小的到前面即可。
选择排序
算法思想
- 选择排序,顾名思义,就是选出来一个进行排序。该算法分为已排序部分和未排序部分。
- 具体而言,对于未排序的部分,遍历出来最小值,让其到最前面,归到已排序的部分。
- 遍历n-1轮后完成整个数组的排序。
动图展示
代码部分
void selectsort(int arr[],int n)
{
int temp;
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
if(arr[j]<arr[i]);
temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
}
int main()
{
int a;
cin>>a;
int *b=new int[a];
for(int i=0;i<a;i++)
{
cin>>b[i];
}
selectsort(b,a);
for(int i=0;i<a;i++)
{
cout<<b[i]<<" ";
}
}
该代码理解起来也比较容易,就不过多叙述了。
插入排序
- 顾名思义,就是对于一个数,把他放到一个合适的位置。整个数组分为已排序部分和未排序部分。
- 初始时,第一个数相当于是有序的,故从第二个数开始插,将其插入到合适的位置。
- 重复上述步骤,直至整个数组均为有序。
动图展示
代码部分
void insertion_sort(int arr[],int len)
{
for(int i=1;i<len;i++)
{
int key=arr[i];
int j=i-1;
while((j>=0)&&(key<arr[j]))
{
arr[j+1]=arr[j];
j--;
}
arr[j+1]=key;
}
}- 第一个for循环中的i表示的对第i个数进行插入操作,往下的j=i-1,是i前面的数。
- 循环体条件((j>=0)&&(key < arr[j])),j是下标,其最小是0,如果key要是比arr[j]小,那么arr[j]就往后移(给key让位置,因为它得往前面插),key再接着比较前面的数。
- 当第j个数不满足循环体条件时,则key就找到位置了,就到第j个数的后面。
希尔排序
Shell Sort是插入排序的一种改进的版本,其先将数组分成若干字数组,对每个子数组进行插入排序,逐步缩小子数组的间隔,最终完成整个数组的排序。
- 先选择一个增量序列,将列表分成若干子列表。
- 对每个子列表进行插入排序。
- 逐步缩小增量,重复上述分组和排序过程,直到增量为1。
代码部分
void shellsort(T array [],int n){
int h=1;
while(h<n/3)
{
h=h*3+1;
}
while(h>=1)
{
for(int i=h;i<n;i++)
{
for(int j=i;j>=h&&array[j]<array[j-h];j-=h)
{
std:swap(array[j],array[j-h]);
}
}
h/=3;
}
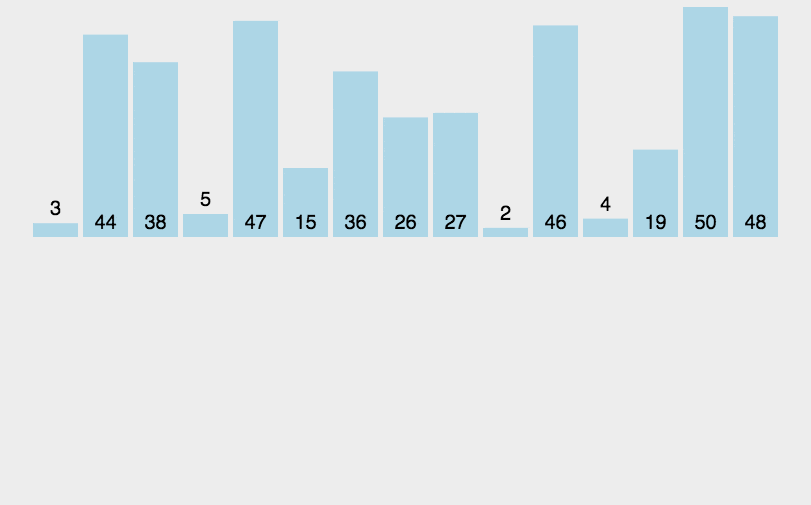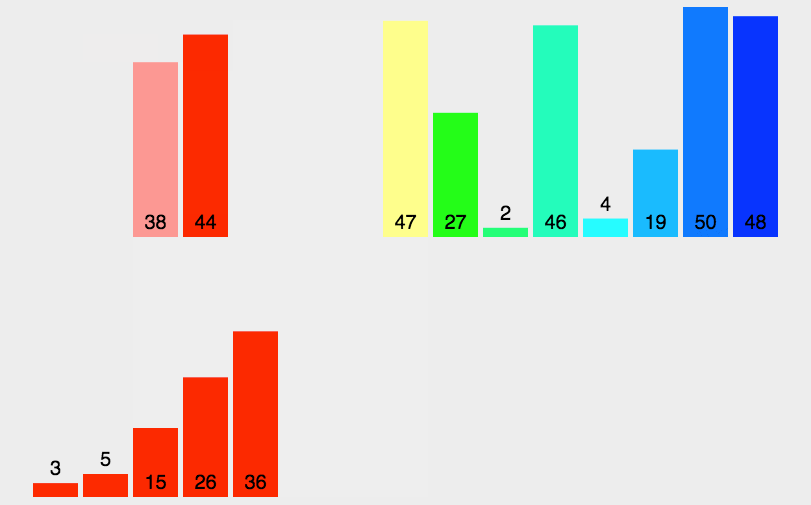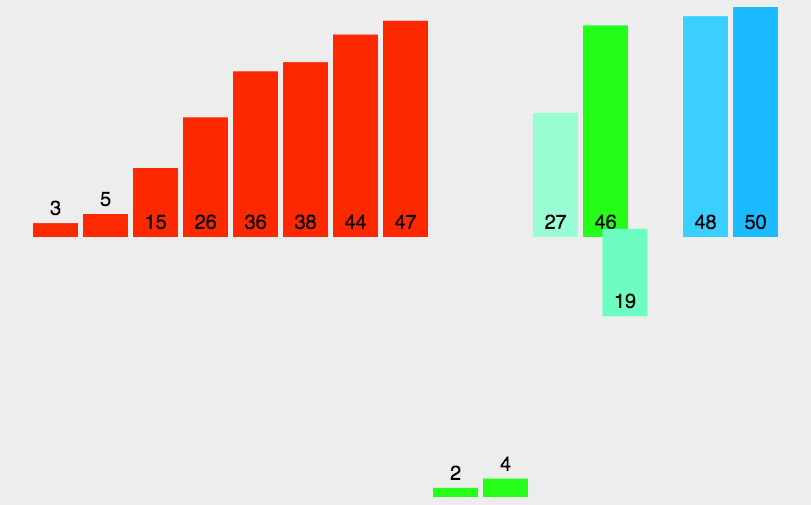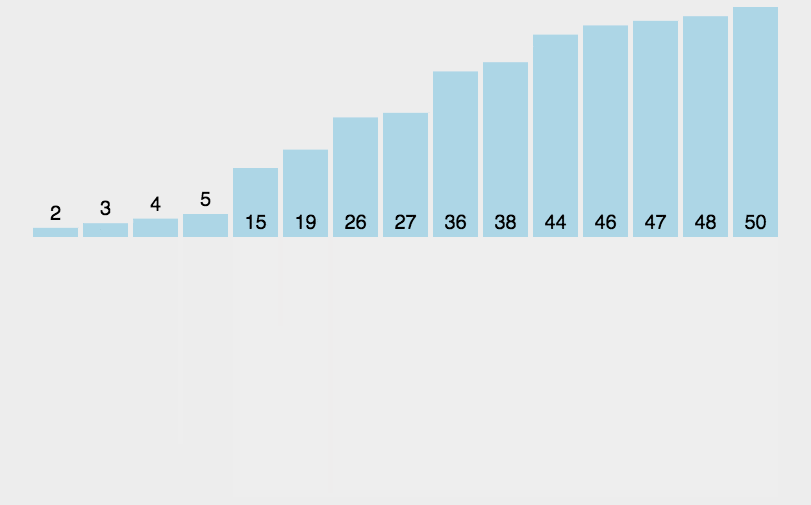
}归并排序
归并排序的核心思想是将一个大问题分解成若干小问题,然后分别解决这些小问题,然后将结果合并起来,最终得到整个问题的解。
算法思想
- 分解:将待排序的数组分成两个子数组,每个子数组包含大约一半的元素。
- 解决,递归的对每个子数组进行排序。
- 合并,将以排序的子数组合并成一个有序的数组。
动图展示
代码部分
1.迭代的方法
void merge_sort(T arr[],int len)
{
T* a=arr;
T* b=new T[len];
for(int seg=1;seg<len;seg+=seg)
{
for(int start=0;start<len;start+=seg*2)
{
int low=start;
int mid=min(start+seg,len);
int high=min(start+seg+seg,len);
int k=low;
int start1=low,end1=mid;
int start2=mid,end2=high;
while(start1<end1&&start2<end2){b[k++]=a[start1]<a[start2]?a[start1++]:a[start2++];}
//如果想要倒序排序的话 while(start1<end1&&start2<end2){b[k++]=a[start1]>a[start2]?a[start1++]:a[start2++];}即可
while(start1<end1){b[k++]=a[start1++];}
while(start2<end2){b[k++]=a[start2++];}
}
T*temp=a;
a=b;
b=temp;
}
if(a!=arr)
{
for(int i=0;i<len;i++)
{
b[i]=a[i];
}
b=a;
}
delete [] b;
}- 先建立了a和b两个指针,一个指向传入数组的首地址,一个指向新建数组的首地址。
- seg可以理解为已序子数组的长度,一开始每个元素可以看成是一个已序的子数组,所以seg开始设为1,每次合并时已序部分的长度会×2。
- start1和start2指向相邻两个已序字数组的第一个元素,下面三个while循环就是将这两个已序子数组合并成一个已序子数组
- 25行的判断语句存在的意义:因为a和b会进行交换,如果交换了奇数次,a会指向新建的数组,b会指向arr,而a是排序好的数组,所以在此把a中的值赋给b,并让b指向a,最后再delete b,这样不会影响到arr。
2.递归的方法
void merge_sort_recursive(int arr[],int reg[],int start,int end){
if (start>=end)
{
return;
}
int len=end-start,mid=start+(len>>1);
int start1=start,end1=mid;
int start2=mid+1,end2=end;
merge_sort_recursive(arr,reg,start1,end1);
merge_sort_recursive(arr,reg,start2,end2);
int k=start;
while(start1<=end1 && start2<=end2){reg[k++]=arr[start1]<arr[start2]?arr[start1++]:arr[start2++];}
while(start1<=end1){reg[k++]=arr[start1++];}
while(start2<=end2){reg[k++]=arr[start2++];}
for(k=start;k<=end;k++)
{
arr[k]=reg[k];
}
}
void merge_sort_recursion(int arr[],const int len)
{
int reg[len];
merge_sort_recursive(arr,reg,0,len-1);
}- 先把整个数组进行分割,划分成两部分,然后对左边这部分进行排序后再对右边这部分进行排序,最后将这两部分进行合并
- 终止条件就是start和end的大小关系,最小的子数组的长度是2,再划分后就会终止,然后对这个子数组排序
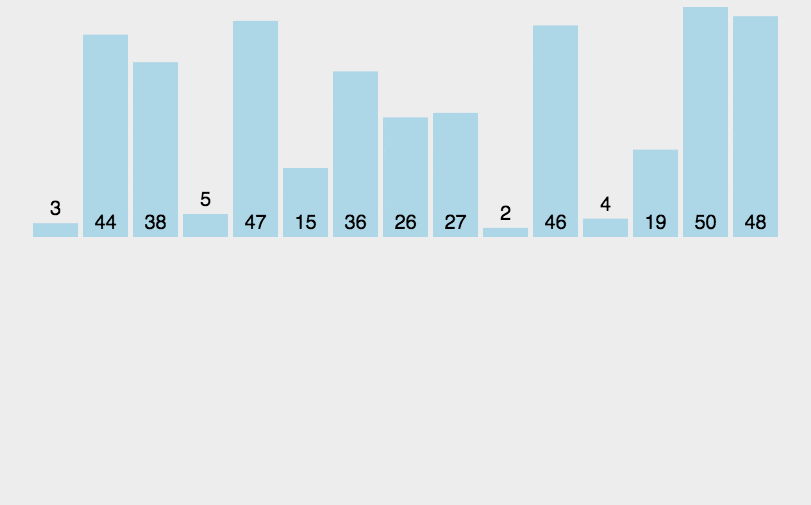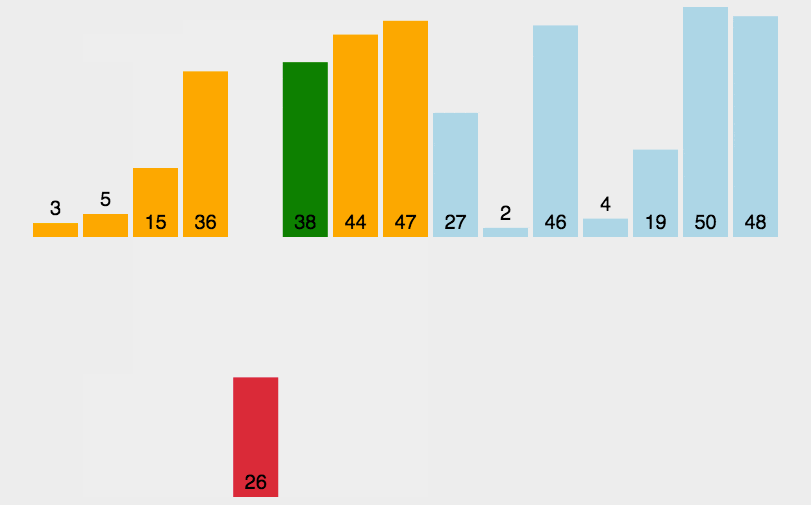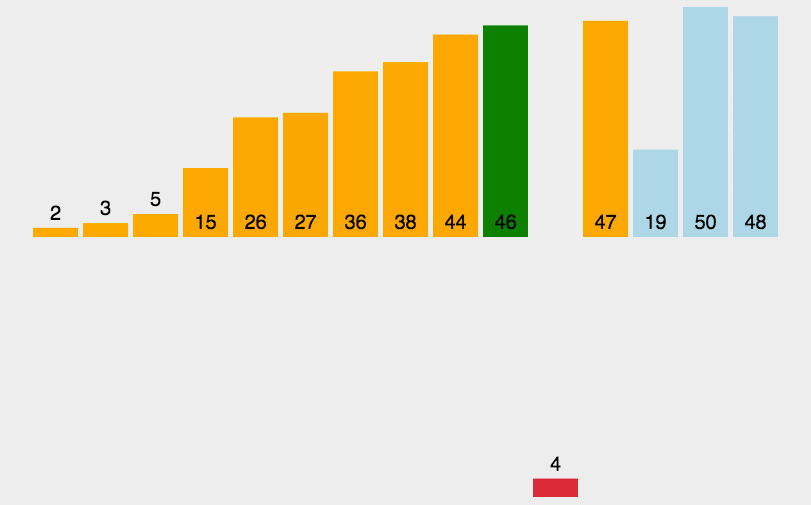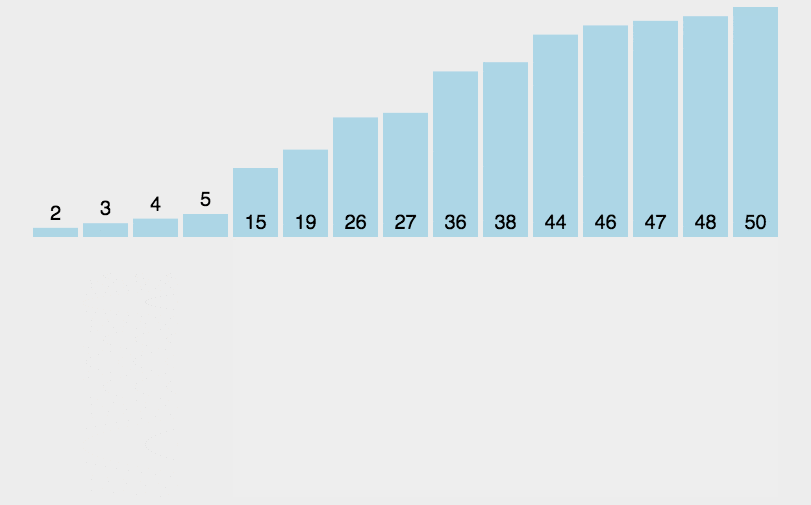
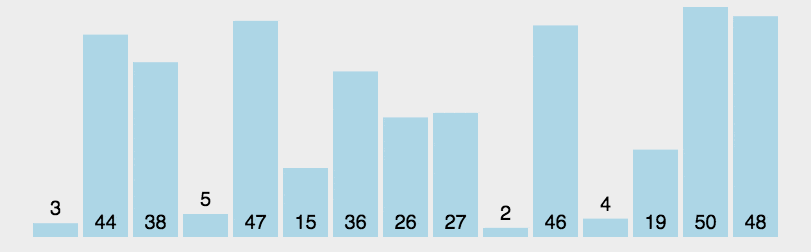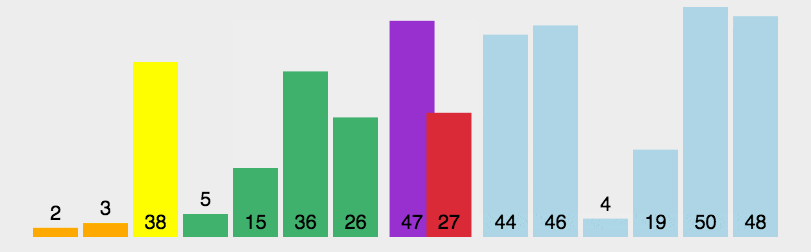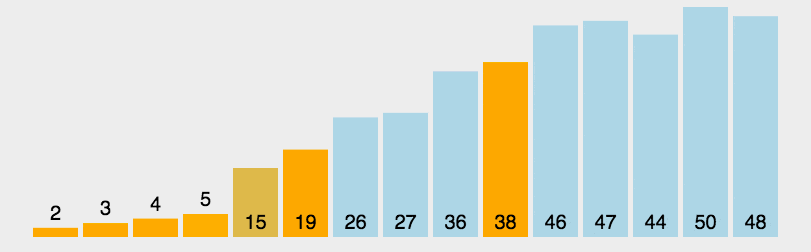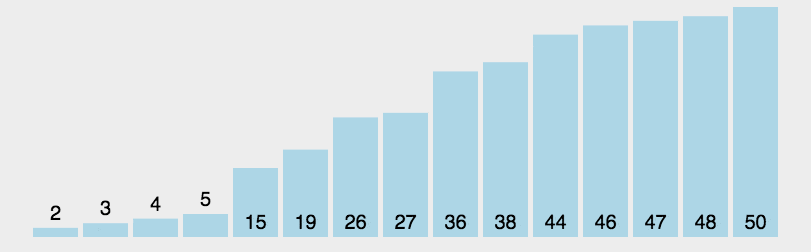
快速排序
Quick Sort是一种高效的排序散发,基于分治法的核心思想。他的核心思想是选择一个基准元素(pivot),将列表分为两部分,一部分小于基准元素,一部分大于基准元素,然后递归地对这两部分进行排序,快速排序的时间复杂度是O(n log n),在实际应用中有优异的性能。
算法思想
- 从列表中随机选择一个元素作为基准(可以随机选择),一下代码中选择的是第一个元素。
- 将列表重新排序,小于基准元素的放到基准的左侧,大于基准元素的放到基准元素的右侧。
- 对基准元素的左侧和右侧的字数组分别进行快速排序
- 递归结束后也就对整个数组进行了排序。
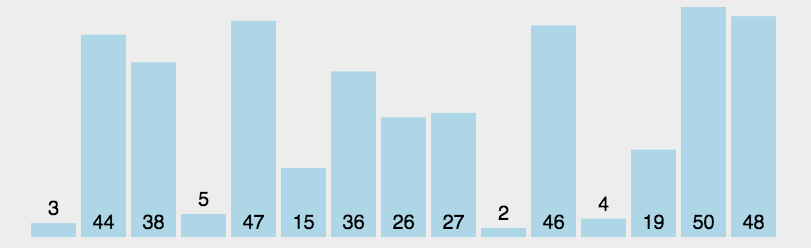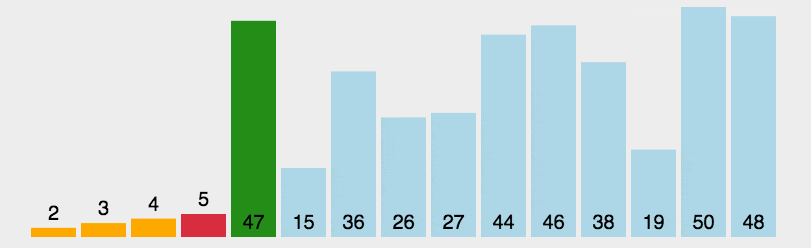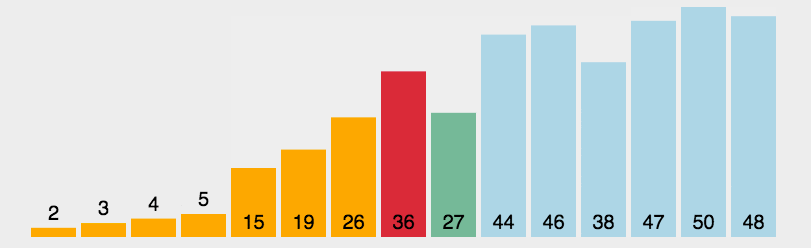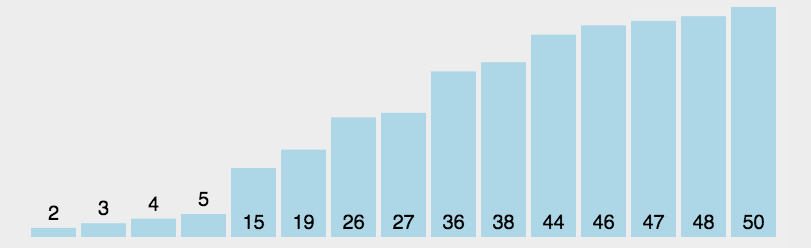
动图展示
代码部分
int Partition(int A[], int left, int right) {
int pivot=A[left];
while(left<right)
{
while(left<right && A[right]>=pivot)
{
right--;
}
A[left]=A[right];
while(left<right && A[left]<=pivot)
{
left++;
}
A[right]=A[left];
}
A[left]=pivot;
return left;
}
// 快速排序函数
void QuickSort(int A[], int low, int high)
{
if(low<high)
{
int pivot=Partition(A,low,high);
QuickSort(A,low,pivot-1);
QuickSort(A,pivot+1,high);
}
}- Partition()这个函数是用于返回选中元素的下标,是一个标准分割数组的函数
- 然后递归的对左侧和右侧进行排序
堆排序
Heapsort是利用堆这种数据结构所设计的一种排序方法。堆积是一种近似完全二叉树,并满足堆积的性质:即子节点的值总是小于(或者大于)它的父节点。
算法步骤
- 先创建一个堆[0…..n-1];
- 把堆首(最大值)和堆尾互换,让堆首成为已序部分;
- 把堆的尺寸缩小1,然后把新的数组顶端的数据调整至相应的部分
- 重复步骤2,直到堆的尺寸为1
动图展示
代码部分
void max_heapify(int arr[],int start,int end)
{
int dad=start;
int son=dad*2+1;
while(son<=end)
{
if(son+1<=end && arr[son+1]>arr[son])
{
son++;
}
if(arr[dad]>arr[son])
{
return;
}
else
{
swap(arr[dad],arr[son]);
dad=son;
son=2*dad+1;
}
}
}
void heap_sort(int arr[],int len) //堆排序
{
for(int i=len/2-1;i>=0;i--)
{
max_heapify(arr,i,len-1);
}
for(int i=len-1;i>=0;i--)
{
swap(arr[0],arr[i]);
max_heapify(arr,0,i-1);
}
}- max_heapify()函数的作用是把从start到end的这些数据形成一个大顶推
- i=len/2-1,代表的是最后一个非叶子结点,第一个for循环的目的就是形成一个堆
- 第二个for循环的目的是把二叉树的最后一个元素和第一个元素交换位置,并去掉归到已序部分,然后max_heapify(arr,0,i-1)是将顶部的元素移动到合适的位置
基数排序
基数排序通过逐位比较元素的每一位(从最低位到最高位)来实现排序,相当于第一次排序将个位数排好,第二次排序将十位数排好,以此类推。
算法步骤
- 找到列表中最大数字的位数,确定需要排序的轮数
- 从最低位开始,依次对每一位进行排序
- 每一轮排序后,更新列表的排序,直到所有位数排序完成
动图展示
代码部分
int maxbit(int data [],int n)
{
int maxdata=data[0];
for(int i=1;i<n;i++)
{
if(maxdata<data[i])
{
maxdata=data[i];
}
}
int d=1;
while(maxdata>=10)
{
maxdata/=10;
d++;
}
return d;
}
void radixsort(int data[],int n)
{
int d=maxbit(data,n);
int *temp=new int[n];
int *count=new int[10];
int i,j,k;
int radix=1;
for(int i=1;i<=d;i++)
{
for(j=0;j<10;j++)
{
count[j]=0;
}
for(j=0;j<n;j++)
{
k=(data[j]/radix)%10;
count[k]++;
}
for(j=1;j<10;j++)
{
count[j]=count[j]+count[j-1];
}
for(j=n-1;j>=0;j--)
{
k=(data[j]/radix)%10;
temp[count[k]-1]=data[j];
count[k]--;
}
for(j=0;j<n;j++)
{
data[j]=temp[j];;
}
radix*=10;
}
delete []temp;
delete []count;
}- maxbit()先return 数组中最大值的位数,temp[]是每轮排序结束后把数据暂时放到这个数组中,count[10]如动图中,底部的10个桶
- 每轮排序前先将桶中的元素清零,然后再根据这一轮中的某一位数将数据放到桶中,接下来的两个for循环是关键,这样确定了排序前的d[j]在排序后应该在temp中的哪个位置,这个设计很巧妙
- 最后再把排序后temp[]中的数值赋给data[]用于下一轮中的排序
桶排序
桶排序是一种分布式算法,它将待排序的元素分配到若干个桶中,然后对每个桶中的元素进行排序,最后将所有桶中的元素按顺序合并
算法步骤
- 根据数据的范围和分布,创建若干个桶
- 遍历待排序的列表,将每个元素分配到对应的同中
- 对每个桶中的元素进行排序
- 将所有桶中的元素按顺序合并,得到最终的排序结果
代码部分
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int BUCKET_NUM = 10;
struct ListNode {
explicit ListNode(int i = 0) : mData(i), mNext(NULL) {}
ListNode* mNext;
int mData;
};
ListNode* insert(ListNode* head, int val) {
ListNode dummyNode;
dummyNode.mNext = head;
ListNode* pre = &dummyNode;
ListNode* curr = head;
ListNode* newNode = new ListNode(val);
while (curr != NULL && curr->mData < val) {
pre = curr;
curr = curr->mNext;
}
newNode->mNext = curr;
pre->mNext = newNode;
return dummyNode.mNext;
}
ListNode* Merge(ListNode* head1, ListNode* head2) {
ListNode dummyNode;
ListNode* tail = &dummyNode;
while (head1 != NULL && head2 != NULL) {
if (head1->mData < head2->mData) {
tail->mNext = head1;
head1 = head1->mNext;
} else {
tail->mNext = head2;
head2 = head2->mNext;
}
tail = tail->mNext;
}
if (head1 != NULL) tail->mNext = head1;
if (head2 != NULL) tail->mNext = head2;
return dummyNode.mNext;
}
void BucketSort(int n, int arr[]) {
vector<ListNode*> buckets(BUCKET_NUM, NULL);
int maxData = *max_element(arr, arr + n);
for (int i = 0; i < n; i++) {
int index = (arr[i] * BUCKET_NUM) / (maxData + 1);
buckets[index] = insert(buckets[index], arr[i]);
}
ListNode* head = buckets[0];
for (int i = 1; i < BUCKET_NUM; i++) {
head = Merge(head, buckets[i]);
}
ListNode* curr = head;
for (int j = 0; j < n; j++) {
arr[j] = curr->mData;
ListNode* temp = curr;
curr = curr->mNext;
delete temp;
}
}- int index=(arr[i]*BUCKET_NUM)/(maxData+1)来确定arr[i]应该分配到那个桶当中(根据桶的个数和最大值来确定)
- 通过链表的插入来对每个桶内的元素排序
- 通过合并链表来有序的合并桶内的元素
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Hwikb!
评论